Forecasting With {epipredict} and Other Advanced Topics

InsightNet Forecasting Workshop 2024


Alice Cima, Rachel Lobay, Daniel McDonald, Ryan Tibshirani

with huge thanks to Logan Brooks, Xueda Shen, and also to Nat DeFries, Dmitry Shemetov, and David Weber

12 December – Afternoon

Outline

  1. Fundamentals of Forecasting

  2. {epipredict}

  3. Customizing arx_forecaster()

  4. Build a Forecaster from Scratch

  5. Advanced Topics

1 Fundamentals of Forecasting

Care with your data

  1. Data splitting
    • Some data you see. You can use it to create your model: Training data.
    • Some data you don’t see. It may arrive later, or you may hold it out to validate your process.
  2. Only training data can be used to create your model.
    • Much more subtle than it sounds.
    • Everything about your model must flow from this
      1. Choosing the model: AR vs ARX, number of lags to use
      2. Estimates of model parameters
      3. How much regularization to use
      4. Any transformations you make of your data

We’ve emphasized most of this already.

But that point about transformations is VERY important. And often overlooked.

Preprocessing correctly

  • A standard proprecessing routine is to scale() each of the predictors.
  • This requires calculating the mean and standard deviation on the training data.
  • And using those values when you make predictions
  • This is hard to do with standard R operations.
chicago_ell <- modeldata::Chicago |>
  select(ridership, temp, humidity, percip) |>
  mutate(across(everything(), scale))


lm(ridership ~ ., data = chicago_ell)

We didn’t save the means and variances.

We need them to process the test data.

We would also need to invert (postprocess) the predictions.

For example: undoing scaling to predict deaths not deaths per 100K population

{tidymodels}

  • The {tidymodels} suite of packages is intended to handle this situation correctly.

  • It’s written by programmers at Posit (the people behind {tidyverse})

  • It doesn’t work for panel data.

  • That’s what we need for Epidemiological Time Series

  • We’ve been working with their team to develop this functionality.

Anatomy of a forecaster

We should build up modular components

Be able to add/remove layers of complexity sequentially, not all at once

We should be able to make preprocessing independent of the model fitting

We should be able to postprocess the predictions

  1. Preprocessor: do things to the data before model training

  2. Trainer: train a model on data, resulting in a fitted model object

  3. Predictor: make predictions, using a fitted model object

  4. Postprocessor: do things to the predictions before returning

2 {epipredict}

{epipredict}

https://cmu-delphi.github.io/epipredict

Installation

# Stable version
pak::pkg_install("cmu-delphi/epipredict@main")


# Development version
# We're using this.
pak::pkg_install("cmu-delphi/epipredict@dev")

What {epipredict} provides (i)

Basic and easy to use “canned” forecasters:

  • Baseline flat forecaster

  • Autoregressive forecaster (ARX)

  • Autoregressive classifier

  • CDC FluSight flatline forecaster

These are supposed to work easily


Handle lots of cases we’ve already seen


We’ll start here

What {epipredict} provides (ii)

  • A framework for creating custom forecasters out of modular components.

  • This is highly customizable, extends {tidymodels} to panel data

  • Good for building a new forecaster from scratch

  • We’ll do an example at the end

  • There are four types of components:

    1. Preprocessor: do things to the data before model training

    2. Trainer: train a model on data, resulting in a fitted model object

    3. Predictor: make predictions, using a fitted model object

    4. Postprocessor: do things to the predictions before returning

Examples of pre-processing

EDA type stuff

  1. Making locations/signals commensurate (scaling)
  2. Dealing with revisions
  3. Detecting and removing outliers
  4. Imputing or removing missing data

Feature engineering

  1. Creating lagged predictors
  2. Day of Week effects
  3. Rolling averages for smoothing
  4. Lagged differences
  5. Growth rates instead of raw signals
  6. The sky’s the limit

Get some data

library(epidatr)
library(epiprocess)
library(epipredict)

cases <- pub_covidcast(
  source = "jhu-csse",
  signals = "confirmed_incidence_num",
  time_type = "day",
  geo_type = "state",
  time_values = epirange(20200401, 20230401),
  geo_values = "*") |>
  select(geo_value, time_value, cases = value)

deaths <- pub_covidcast(
  source = "jhu-csse",
  signals = "deaths_incidence_num",
  time_type = "day",
  geo_type = "state",
  time_values = epirange(20200401, 20230401),
  geo_values = "*") |>
  select(geo_value, time_value, deaths = value)

cases_deaths <- full_join(cases, deaths, by = c("time_value", "geo_value")) |>
  as_epi_df()

Pre-processing: data scaling

Scale cases and deaths by population and multiply by 100K

cases_deaths <- left_join(
  x = cases_deaths,
  y = state_census |> select(pop, abbr),   # state_census is available in epipredict
  by = join_by(geo_value == abbr)
) |>
  mutate(
    cases = cases / pop * 1e5, 
    deaths = deaths / pop * 1e5
  ) |> 
  select(-pop)

Scaled COVID cases and deaths

Code 
cases_deaths |> 
  filter(geo_value %in% c("ca", "ma", "ny", "tx")) |>
  autoplot(cases, deaths) +
  scale_color_delphi(name = "") +
  xlab("Reference date")

Pre-processing: smoothing

Smooth the data by computing 7-day averages of cases and deaths for each state

cases_deaths <- cases_deaths |>
  group_by(geo_value) |>
  epi_slide(
    cases_7dav = mean(cases, na.rm = TRUE),
    deaths_7dav = mean(deaths, na.rm = TRUE),
    .window_size = 7
  ) |>
  ungroup() |>
  mutate(cases = NULL, deaths = NULL) |>
  rename(cases = cases_7dav, deaths = deaths_7dav)

Scaled and smoothed COVID cases deaths

Code 
cases_deaths |> 
  filter(geo_value %in% c("ca", "ma", "ny", "tx")) |>
  autoplot(cases, deaths)  +
  scale_color_delphi(name = "") +
  xlab("Reference date")

Pre-processing: fix outliers and negative values

Code 
deaths_outlr <- cases_deaths |> 
  group_by(geo_value) |>
  mutate(outlr = detect_outlr_rm(time_value, deaths, detect_negatives = TRUE)) |>
  unnest(outlr) |>
  ungroup()

Fit arx_forecaster on training set

  • Back to the ARX(1) model for COVID deaths: \(\quad \hat y_{t+28} = \hat\phi + \hat\phi_0 y_{t} + \hat\beta_0 x_{t}\)

  • Only focus on California (for now)

  • Using {epipredict}

# split into train and test 
ca <- cases_deaths |> filter(geo_value == "ca")
t0_date <- as.Date('2021-04-01')
train <- ca |> filter(time_value <= t0_date)
test <- ca |> filter(time_value > t0_date)

# fit ARX
epi_arx <- arx_forecaster(
  epi_data = train |> as_epi_df(), 
  outcome = "deaths", 
  predictors = c("cases", "deaths"),
  trainer = linear_reg(),
  args_list = arx_args_list(lags = 0, ahead = 28, quantile_levels = c(0.1, 0.9))
)

arx_forecaster output

  • A workflow object which can be used any time in the future to create forecasts ($epi_workflow).
    • All necessary preprocessing; both the sequence of steps, and any necessary statistics
    • The fitted model object
    • The sequence of steps for postprocessing
  • A forecast (point prediction + interval) for 28 days after the last available time value in the data ($predictions).

arx_forecaster output

epi_arx 
══ A basic forecaster of type ARX Forecaster ═══════════════════════════════════
This forecaster was fit on 2024-12-12 00:10:36.
Training data was an <epi_df> with:
• Geography: state,
• Time type: day,
• Using data up-to-date as of: 2024-12-12 00:09:47.
• With the last data available on 2021-04-01
── Predictions ─────────────────────────────────────────────────────────────────
A total of 1 prediction is available for
• 1 unique geographic region,
• At forecast date: 2021-04-01,
• For target date: 2021-04-29,

Extract fitted object

epi_arx$epi_workflow
══ Epi Workflow [trained] ══════════════════════════════════════════════════════
Preprocessor: Recipe
Model: linear_reg()
Postprocessor: Frosting
── Preprocessor ────────────────────────────────────────────────────────────────
6 Recipe steps.
1. step_epi_lag()
2. step_epi_lag()
3. step_epi_ahead()
4. step_naomit()
5. step_naomit()
6. step_training_window()
── Model ───────────────────────────────────────────────────────────────────────

Call:
stats::lm(formula = ..y ~ ., data = data)

Coefficients:
 (Intercept)   lag_0_cases  lag_0_deaths  
    0.075387      0.009953      0.201329  
── Postprocessor ───────────────────────────────────────────────────────────────
5 Frosting layers.
1. layer_predict()
2. layer_residual_quantiles()
3. layer_add_forecast_date()
4. layer_add_target_date()
5. layer_threshold()

$epi_workflow

Contains information on

  • Pre-processing steps automatically performed by arx_forecaster (e.g. compute lags of the predictors)

  • Fitted model

  • Post-processing steps automatically performed by arx_forecaster (e.g. compute quantiles)

Extract predictions

epi_arx$predictions
# A tibble: 1 × 5
  geo_value .pred        .pred_distn forecast_date target_date
  <chr>     <dbl>             <dist> <date>        <date>     
1 ca        0.218 quantiles(0.22)[2] 2021-04-01    2021-04-29

Note

  • .pred_distn is actually a “distribution”, parameterized by its quantiles

  • arx_forecaster estimates the quantiles in a different way than lm

Extract predictions

We can extract the distribution into a “long” epi_df

epi_arx$predictions |>
  pivot_quantiles_longer(.pred_distn)
# A tibble: 2 × 6
  geo_value .pred values quantile_levels forecast_date target_date
  <chr>     <dbl>  <dbl>           <dbl> <date>        <date>     
1 ca        0.218  0.137             0.1 2021-04-01    2021-04-29 
2 ca        0.218  0.300             0.9 2021-04-01    2021-04-29

or into a “wide” epi_df

epi_arx$predictions |>
  pivot_quantiles_wider(.pred_distn)
# A tibble: 1 × 6
  geo_value .pred forecast_date target_date `0.1` `0.9`
  <chr>     <dbl> <date>        <date>      <dbl> <dbl>
1 ca        0.218 2021-04-01    2021-04-29  0.137 0.300

Predict with fitted ARX (split-sample)

  • arx_forecaster fits a model to the training set, and outputs only one prediction (for time \(t_0+h\)).

  • To get predictions for the test set:

predict(epi_arx$epi_workflow, test)
An `epi_df` object, 707 x 6 with metadata:
* geo_type  = state
* time_type = day
* as_of     = 2024-12-12 00:09:47.499248

# A tibble: 707 × 6
   geo_value time_value .pred        .pred_distn forecast_date target_date
 * <chr>     <date>     <dbl>             <dist> <date>        <date>     
 1 ca        2021-04-02 0.213 quantiles(0.21)[2] 2021-04-01    2021-04-29 
 2 ca        2021-04-03 0.202  quantiles(0.2)[2] 2021-04-01    2021-04-29 
 3 ca        2021-04-04 0.197  quantiles(0.2)[2] 2021-04-01    2021-04-29 
 4 ca        2021-04-05 0.201  quantiles(0.2)[2] 2021-04-01    2021-04-29 
 5 ca        2021-04-06 0.199  quantiles(0.2)[2] 2021-04-01    2021-04-29 
 6 ca        2021-04-07 0.195  quantiles(0.2)[2] 2021-04-01    2021-04-29 
 7 ca        2021-04-08 0.195  quantiles(0.2)[2] 2021-04-01    2021-04-29 
 8 ca        2021-04-09 0.196  quantiles(0.2)[2] 2021-04-01    2021-04-29 
 9 ca        2021-04-10 0.208 quantiles(0.21)[2] 2021-04-01    2021-04-29 
10 ca        2021-04-11 0.213 quantiles(0.21)[2] 2021-04-01    2021-04-29 
# ℹ 697 more rows

Predict with ARX (when re-fitting)

  • In practice, if we want to re-train the forecasters as new data arrive, we fit and predict combining arx_forecaster with epix_slide

  • From now on, we will only used versioned data, and make predictions once a week

Predict with ARX (re-fitting on trailing window)

h <- 28         # horizon
w <- 120 + h    # trailing window length

# Specify the forecast dates
fc_time_values <- seq(from = t0_date, to = as.Date("2023-02-09"), by = "1 week")

# Slide the arx_forecaster over the epi_archive
pred_arx <- ca_archive |> epix_slide(
  ~ arx_forecaster(epi_data = .x,
                   outcome = "deaths", 
                   predictors = c("cases", "deaths"), 
                   trainer = linear_reg(),
                   args_list = arx_args_list(lags = 0, ahead = h, quantile_levels = c(0.1, 0.9))
  )$predictions |>
    pivot_quantiles_wider(.pred_distn),
  .before = w, 
  .versions = fc_time_values
)

Predict with ARX

Note (window length)

We set \(w = 120 + h\) to match the window size of the ARX model we fitted manually.

When considering a window from \(t-w\) to \(t\), we had access to all outcomes in that window, and to all predictors between \(t-w-h\) and \(t-h\).

(That’s because we lagged \(x\) before applying the window.)

So we were “cheating” by saying that the trailing window had length \(w=120\), as its actual size was \(120+h\)!

Note (all past)

The method fitting on all past data up to the forecasting date can be implemented by setting:

.before = Inf in epix_slide().

Predict with ARX (re-fitting on trailing window)

pred_arx 
# A tibble: 98 × 7
   version    geo_value  .pred forecast_date target_date  `0.1` `0.9`
 * <date>     <chr>      <dbl> <date>        <date>       <dbl> <dbl>
 1 2021-04-01 ca        0.396  2021-03-31    2021-04-28  0.192  0.599
 2 2021-04-08 ca        0.395  2021-04-07    2021-05-05  0.197  0.594
 3 2021-04-15 ca        0.403  2021-04-14    2021-05-12  0.211  0.595
 4 2021-04-22 ca        0.312  2021-04-21    2021-05-19  0.142  0.482
 5 2021-04-29 ca        0.261  2021-04-28    2021-05-26  0.0879 0.433
 6 2021-05-06 ca        0.209  2021-05-05    2021-06-02  0.0238 0.394
 7 2021-05-13 ca        0.158  2021-05-12    2021-06-09  0      0.345
 8 2021-05-20 ca        0.118  2021-05-19    2021-06-16  0      0.296
 9 2021-05-27 ca        0.0775 2021-05-26    2021-06-23  0      0.239
10 2021-06-03 ca        0.0552 2021-06-02    2021-06-30  0      0.137
# ℹ 88 more rows

Predict with ARX (re-fitting on trailing window)

        MAE     MASE  Coverage
 0.07889637 264.5207 0.4285714

Customizing arx_forecaster()

arx_forecaster(
  epi_data = train, 
  outcome = "deaths", 
  predictors = c("cases", "deaths"),
  trainer = linear_reg() |> set_engine("lm"),
  args_list = arx_args_list(lags = 0, ahead = 28, quantile_levels = c(0.1, 0.9))
)

  • Modify predictors to add/drop predictors

    • e.g. drop deaths for regression with a lagged predictor, or drop cases to get AR model

    • default: predictors = outcome

Customizing arx_forecaster()

arx_forecaster(
  epi_data = train, 
  outcome = "deaths", 
  predictors = c("cases", "deaths"),
  trainer = linear_reg(),
  args_list = arx_args_list(lags = 0, ahead = 28, quantile_levels = c(0.1, 0.9))
)
  • Modify arx_args_list to change lags, horizon, quantile levels, …
arx_args_list(
  lags = c(0L, 7L, 14L),
  ahead = 7L,
  n_training = Inf,
  forecast_date = NULL,
  target_date = NULL,
  adjust_latency = c("none", "extend_ahead", "extend_lags", "locf"),
  warn_latency = TRUE,
  quantile_levels = c(0.05, 0.95),
  symmetrize = TRUE,
  nonneg = TRUE,
  quantile_by_key = character(0L),
  check_enough_data_n = NULL,
  check_enough_data_epi_keys = NULL,
  ...
)

Customizing arx_forecaster

Change predictors: doctor visits instead of cases

dv_archive <- pub_covidcast(
  source = "doctor-visits",
  signals = "smoothed_adj_cli",
  time_type = "day",
  geo_type = "state",
  time_values = epirange(20200401, 20230401),
  geo_values = "*",
  issues = epirange(20200401, 20230401)) |>
  select(geo_value, time_value, version = issue, doctor_visits = value) |>
  arrange(geo_value, time_value) |>
  as_epi_archive(compactify = FALSE)

Customizing arx_forecaster

Change predictors: doctor visits instead of cases

pred_arx_hosp <- ca_archive_dv |> epix_slide(
  ~ arx_forecaster(epi_data = .x,
                   outcome = "deaths", 
                   predictors = c("deaths", "doctor_visits"), 
                   trainer = linear_reg(),
                   args_list = arx_args_list(lags = 0, ahead = 28, quantile_levels = c(0.1, 0.9))
  )$predictions |>
    pivot_quantiles_wider(.pred_distn),
  .before = w, 
  .versions = fc_time_values
)

Predictions (doctor visits instead of cases in predictor set)

        MAE     MASE  Coverage
 0.06040473 202.5227 0.5510204

Customizing arx_forecaster

Add more lags

pred_arx_more_lags <- ca_archive_dv |> epix_slide(
  ~ arx_forecaster(epi_data = .x,
                   outcome = "deaths", 
                   predictors = c("deaths", "doctor_visits"), 
                   trainer = linear_reg(),
                   args_list = arx_args_list(
                     lags = c(0, 7, 14), 
                     ahead = 28, quantile_levels = c(0.1, 0.9)
                   )
  )$predictions |>
    pivot_quantiles_wider(.pred_distn),
  .before = w, 
  .versions = fc_time_values
)

Predictions (more lags)

      MAE     MASE  Coverage
 0.077735 260.6269 0.3367347

Customizing arx_forecaster

Multiple horizons

forecast_times <- seq(from = t0_date, to = as.Date("2023-02-23"), by = "1 month")
pred_h_days_ahead <- function(epi_archive, ahead = 7) {
  epi_archive |>
    epix_slide(
      ~ arx_forecaster(epi_data = .x,
                       outcome = "deaths", 
                       predictors = c("deaths", "doctor_visits"), 
                       trainer = linear_reg() |> set_engine("lm"),
                       args_list = arx_args_list(
                         lags = 0,  
                         ahead = ahead,
                         quantile_levels = c(0.1, 0.9))
      )$predictions |> 
        pivot_quantiles_wider(.pred_distn),
  .before = w, 
  .versions = forecast_times
  )
}
h <- c(7, 14, 21, 28)
forecasts <- bind_rows(map(h, ~ pred_h_days_ahead(ca_archive_dv, ahead = .x)))

Predictions (multiple horizons)

3 Advanced Customizations

Changing trainer

arx_forecaster(epi_data = train |> as_epi_df(), 
               outcome = "deaths", 
               predictors = c("cases", "deaths"),
               trainer = linear_reg() |> set_engine("lm"),
               args_list = arx_args_list(lags = 0, ahead = 28,
                                         quantile_levels = c(0.1, 0.9)))

Modify trainer to use a model that is not lm (default)

  • e.g. trainer = rand_forest()
  • can use any {parsnip} models, see list
  • {epipredict} has a number of custom engines as well

Changing trainer

pred_arx_rf <- ca_archive_dv |>
  epix_slide(
    ~ arx_forecaster(epi_data = .x,
                     outcome = "deaths", 
                     predictors = c("deaths", "doctor_visits"), 
                     trainer = parsnip::rand_forest(mode = "regression"), # defaults to ranger
                     args_list = arx_args_list(
                       lags = 0,
                       ahead = 28,
                       quantile_levels = c(0.1, 0.9))
                     )$predictions |>
        pivot_quantiles_wider(.pred_distn),
  .before = w, 
  .versions = fc_time_values
)

Predictions (trained using random forest)

        MAE     MASE  Coverage
 0.08028482 269.1759 0.1020408

Warning!

  • Random forests has really poor coverage here.

  • The reason is the way intervals are calculated.

  • Can change engine to get better coverage:

specify engine = "grf_quantiles" in the rand_forest call

Predictions from a random forest with grf_quantiles

        MAE     MASE  Coverage
 0.08824774 295.8736 0.3979592

Geo-pooling

  • When we observe data over time from multiple locations (e.g. states or counties).


  • We could

    • Estimate coefficients separately for each location (as we have done so far), or
    • Fit one model using all locations together at each time point (geo-pooling).
    • Estimated coefficients will not be location specific.


  • We will now pool data from all US states to make predictions.

Geo-pooling

pred_arx_geo_pool <- usa_archive_dv |> epix_slide(
  ~ arx_forecaster(epi_data = .x,
                   outcome = "deaths", 
                   predictors = c("deaths", "doctor_visits"), 
                   args_list = arx_args_list(lags = 0, ahead = 28, quantile_levels = c(0.1, 0.9))
  )$predictions |>
    pivot_quantiles_wider(.pred_distn),
  .before = w, 
  .versions = fc_time_values
)

Note: geo-pooling is the default in epipredict

Predictions (geo-pooling, \(h=28\))

         MAE     MASE  Coverage
CA 0.1342220 450.0143 0.8673469
MA 0.1200344 296.9929 0.8041237
NY 0.1328566 327.4008 0.8556701
TX 0.1601115 343.0498 0.8350515

Predict without geo-pooling

pred_arx_no_geo_pool <- function(archive, ahead = 28, lags = 0){
  archive |>
    epix_slide(
      ~ group_by(.x, geo_value) |> 
        group_map(.keep = TRUE, function(group_data, group_key) {
          arx_forecaster(epi_data = group_data,
                         outcome = "deaths", 
                         predictors = c("deaths", "doctor_visits"), 
                         trainer = linear_reg() |> set_engine("lm"),
                         args_list = arx_args_list(
                           lags = lags,
                           ahead = ahead,
                           quantile_levels = c(0.1, 0.9))
                         )$predictions |>
            pivot_quantiles_wider(.pred_distn)
        }) |>
        list_rbind(),
    .before = w, 
    .versions = fc_time_values
    )}

pred_no_geo_pool_28 <- pred_arx_no_geo_pool(usa_archive_dv$DT |> 
                                              filter(geo_value %in% c("ca", "ma", "ny", "tx")) |> 
                                              as_epi_archive())

Predictions (without geo-pooling, \(h=28\))

          MAE     MASE  Coverage
CA 0.06040473 202.5227 0.5510204
MA 0.33532528 823.3607 0.3367347
NY 0.21072571 516.3337 0.5408163
TX 0.14144058 306.2029 0.4285714

Geo-pooling or not?

  • Geo-pooled predictions tend to be more stable

  • Generally with wider intervals (and better coverage)

  • Meanwhile, predictions from state-wise models tend to be more volatile

The extent to which this occurs differs based on the horizon.

Previously we studied \(h=28\). What happens for \(h=7\)?

Predictions (geo-pooling, \(h = 7\))

          MAE     MASE  Coverage
CA 0.09676644 320.9851 0.9081633
MA 0.09278403 234.9664 0.8350515
NY 0.09029822 222.3488 0.9381443
TX 0.11307616 239.1528 0.8659794

Predictions (without geo-pooling, \(h=7\))

          MAE     MASE  Coverage
CA 0.03971988 131.7553 0.6734694
MA 0.06579422 168.3530 0.5714286
NY 0.05005395 124.5359 0.6836735
TX 0.05756194 122.0824 0.7040816

What are these ARX intervals?

  • {epipredict} takes quantiles of training residuals to form its prediction intervals
  • In comparison to traditional (parametric) intervals from lm(), this is more flexible
  • It can in principle adapt to asymmetric or heavy-tailed error distributions


Taking quantiles of training residuals can be problematic if the model is overfit.


Quantile regression provides an alternative, wherein we estimate these quantiles directly

Technically, grf_quantiles was using Quantile Loss with Random Forests

Quantile regression

Now we directly target conditional quantiles of the outcome over time.

Estimating tail quantiles requires more data, so

  • unsuitable for settings with small training set (e.g. trailing window on one state)

  • can benefit by combination with geo-pooling (much more data to train on)

library(quantreg)

pred_qr_geo_pool <- usa_archive_dv |>
  epix_slide(
    ~ arx_forecaster(epi_data = .x,
                     outcome = "deaths", 
                     predictors = c("deaths", "doctor_visits"), 
                     trainer = quantile_reg(),
                     args_list = arx_args_list(
                       lags = 0, 
                       ahead = 28,
                       quantile_levels = c(0.1, 0.9))
                     )$predictions |>
        pivot_quantiles_wider(.pred_distn),
  .before = w, 
  .versions = fc_time_values
)

Predictions (geo-pooling + quantile regression, \(h=28\))

         MAE     MASE  Coverage
CA 0.1447173 485.2027 0.8877551
MA 0.1214715 300.5488 0.7216495
NY 0.1384252 341.1235 0.7525773
TX 0.1604103 343.6901 0.7835052

Predictions (geo-pooling + linear regression, \(h=28\))

         MAE     MASE  Coverage
CA 0.1342220 450.0143 0.8673469
MA 0.1200344 296.9929 0.8041237
NY 0.1328566 327.4008 0.8556701
TX 0.1601115 343.0498 0.8350515

4 Build a forecaster from scratch

Build a forecaster from scratch

  • So far, we performed manual pre-processing,

  • and then relied on a canned forecaster

  • to automatically perform more pre-processing, training, predicting, and post-processing.

What if we want more direct control on each single step?

Under the hood of arx_forecaster()

# A preprocessing "recipe" that turns raw data into features / response
rec <- epi_recipe(ca) |>
  step_epi_lag(cases, lag = c(0, 7, 14)) |>
  step_epi_lag(deaths, lag = c(0, 7, 14)) |>
  step_epi_ahead(deaths, ahead = 28) |>
  step_epi_naomit()

# Training engine
eng <- quantile_reg(quantile_levels = c(.1, .5, .9))

# A post-processing routine describing what to do to the predictions
frost <- frosting() |>
  layer_predict() |>
  layer_threshold(.pred, lower = 0) |> # predictions / intervals should be non-negative
  layer_add_target_date() |>
  layer_add_forecast_date()

# Bundle up the preprocessor, training engine, and postprocessor
# We use quantile regression
ewf <- epi_workflow(rec, eng, frost)

# Fit it to data (we could fit this to ANY data that has the same format)
trained_ewf <- fit(ewf, data = ca)

# Make predictions from the end of our training data
# we could have made predictions using the same model on ANY test data
fcasts <- forecast(trained_ewf)

Predicting influenza hospitalizations

  • Current task: predict influenza hospitalizations for all states + DC + PR.
  • Forecasts submitted to CDC Flusight Forecast Hub

Specifically:

  1. From November 20, 2024 until May 31, 2025
  2. Every Wednesday at 11pm EDT
  3. Predict 0, 1, 2, 3 epiweeks ahead
  4. Point forecast + 23 quantiles
  5. Response is NHSN Weekly Hospitalizations

From here on, the emphasis is “how” to make these adjustments. Ran out of time to evaluate!

Aside: data issues

  • Hospital reporting was down for a period over the summer.

  • The current data doesn’t seem to match the historical data very well.

We don’t know if we trust the data yet enough

  • It may get revised significantly

  • Let’s do something super simple, until we’re more confident

Climatological forecaster
For a given epiweek, predict the historical quantiles
Make adjustments to address the fact that we have some new data
Privledge the history

Think like the weather: “what is the typical weather in February in Georgia, that’s our forecast”

Climatological forecaster

climatological_model <- function(epi_data, forecast_date, ahead, window_size = 3, geo_agg = FALSE) {
  forecast_week <- epiweek(forecast_date)
  last_date_data <- max(epi_data$time_value)
  probs <- c(.1, .5, .9)
  filtered <- epi_data |> 
    filter(
      (season != "2020/21") & (season != "2021/22"), # drop weird years
      # keep data either within the window, or within the past window weeks
      (abs(forecast_week + ahead - epiweek) <= window_size) |
        (last_date_data - time_value <= window_size * 7)
    )
  if (geo_agg) {
    filtered <- filtered |>
      left_join(state_census |> select(geo_value = abbr, pop), by = "geo_value") |>
      mutate(nhsn = nhsn / pop * 1e5) %>%
      select(geo_value, epiweek, epiyear, season, season_week, nhsn, pop)
  } else {
    filtered <- filtered |> group_by(geo_value)
  }
  naive_preds <- filtered |> reframe(enframe(
    quantile(nhsn, probs = probs, na.rm = TRUE, type = 8), name = "quantile"
  )) |>
    mutate(
      forecast_date = forecast_date,
      target_end_date = forecast_date + ahead * 7,
      quantile = as.numeric(sub("%", "", quantile)) / 100,
      value = pmax(0, value)
    )
  if (geo_agg) {
    naive_preds <- naive_preds |>
      expand_grid(filtered |> distinct(geo_value, pop)) |>
      mutate(value = value * pop / 1e5) |>
      select(-pop) |>
      select(geo_value, forecast_date, target_end_date, quantile, value) |>
      arrange(geo_value, forecast_date, target_end_date)
  }
  naive_preds |> ungroup() |> mutate(value = pmax(0, value))
}

Climate predictions for this week

Almost our production forecaster (helper functions)

roll_modular_multivec <- function(col, index, window_size, modulus = 53) {
  tib <- tibble(col = col, index = index) |>
    arrange(index) |>
    tidyr::nest(data = col, .by = index)
  out <- double(nrow(tib))
  for (iter in seq_along(out)) {
    entries <- (iter - window_size):(iter + window_size) %% modulus
    entries[entries == 0] <- modulus
    out[iter] <- with(
      purrr::list_rbind(tib$data[entries]),
      median(col, na.rm = TRUE)
    )
  }
  tibble(index = unique(tib$index), climate_pred = out)
}

climatological_feature <- function(epi_data, window_size = 3) {
  epi_data |>
    filter(season != "2020/21", season != "2021/22") |> # drop weird years)
    select(nhsn, epiweek, geo_value) |>
    reframe(roll_modular_multivec(nhsn, epiweek, window_size, 53), .by = geo_value) |>
    mutate(climate_pred = pmax(0, climate_pred)) |>
    rename(epiweek = index)
}

Almost our production forecaster (data munging)

climate <- climatological_feature(climate_data |> select(nhsn, epiweek, season, geo_value))
nssp <- pub_covidcast( # time_value is first day of the epiweek
  source = "nssp",
  signal = "pct_ed_visits_influenza",
  time_type = "week",
  geo_type = "state",
  geo_values = "*"
) |>
  select(geo_value, time_value, nssp = value)

flu_data <- hhs_v_nhsn |>
  select(time_value, geo_value, hhs = new_source) |>
  left_join(nssp |> mutate(time_value = time_value + 6), by = join_by(geo_value, time_value))

n_geos <- n_distinct(flu_data$geo_value)
max_time_value <- max(flu_data$time_value)
empty_data <- tibble(
  time_value = rep(max_time_value + days(1:3 * 7), each = n_geos),
  geo_value = rep(unique(flu_data$geo_value), times = 3),
  nssp = NA, hhs = NA
)

flu_data <- flu_data |>
  filter(month(time_value) %in% 8:12, year(time_value) %nin% c(2020, 2021)) |>
  add_row(empty_data) |>
  mutate(epiweek = epiweek(time_value)) |>
  left_join(climate, by = join_by(geo_value, epiweek)) |>
  select(!epiweek) |>
  filter(geo_value %nin% c("as", "vi", "gu", "mp", "usa")) |>
  arrange(geo_value, time_value) |>
  as_epi_df()

Almost our production forecaster (workflow)

r <- epi_recipe(flu_data) |>
  step_population_scaling(
    hhs, nssp,
    df = epidatasets::state_census,
    df_pop_col = "pop",
    create_new = FALSE,
    rate_rescaling = 1e5,
    by = c("geo_value" = "abbr")) |>
  recipes::step_mutate(hhs = hhs^(1/4), nssp = nssp^(1/4), climate_pred = climate_pred^(1/4)) |>
  step_epi_lag(hhs, lag = c(0, 7, 14)) |>
  step_epi_lag(nssp, lag = c(0, 7, 14)) |>
  step_epi_ahead(hhs, ahead = 21) |>
  step_epi_ahead(climate_pred, ahead = 21, role = "predictor") |>
  step_epi_naomit()

e <- quantile_reg(quantile_levels = c(0.1, 0.25, 0.5, 0.75, 0.9)) 

f <- frosting() |>
  layer_predict() |>
  layer_threshold(.pred, lower = 0)
ewf <- epi_workflow(r, e, f)
trained_ewf <- ewf |> fit(flu_data)

preds <- forecast(trained_ewf) |>
  left_join(epidatasets::state_census |> select(pop, abbr), join_by(geo_value == abbr)) |>
  mutate(
    .pred = .pred^4 * pop / 1e5,
    forecast_date = time_value + days(7),
    target_date = forecast_date + days(14),
    time_value = NULL,
    pop = NULL
  )

Plot our forecasts

5 Advanced Topics

Ensembling

Instead of choosing one model, we can combine the predictions from multiple base models. Ensemble types:

  • untrained: combine base models, agnostic to past performance

  • trained: weight base models, accounting for past performance

Simplest untrained method: simple average of base model forecasts

\[ \hat{y}^{\text{avg}}_{t+h|t} = \frac{1}{p} \sum_{j=1}^p \hat{y}^j_{t+h|t} \]

A more robust option: simple median of base model forecasts

\[ \hat{y}^{\text{med}}_{t+h|t} = \mathrm{median}\Big\{ \hat{y}^j_{t+h|t} : j = 1,\dots,p \Big\} \]

Example from the Covid-19 Forecast Hub

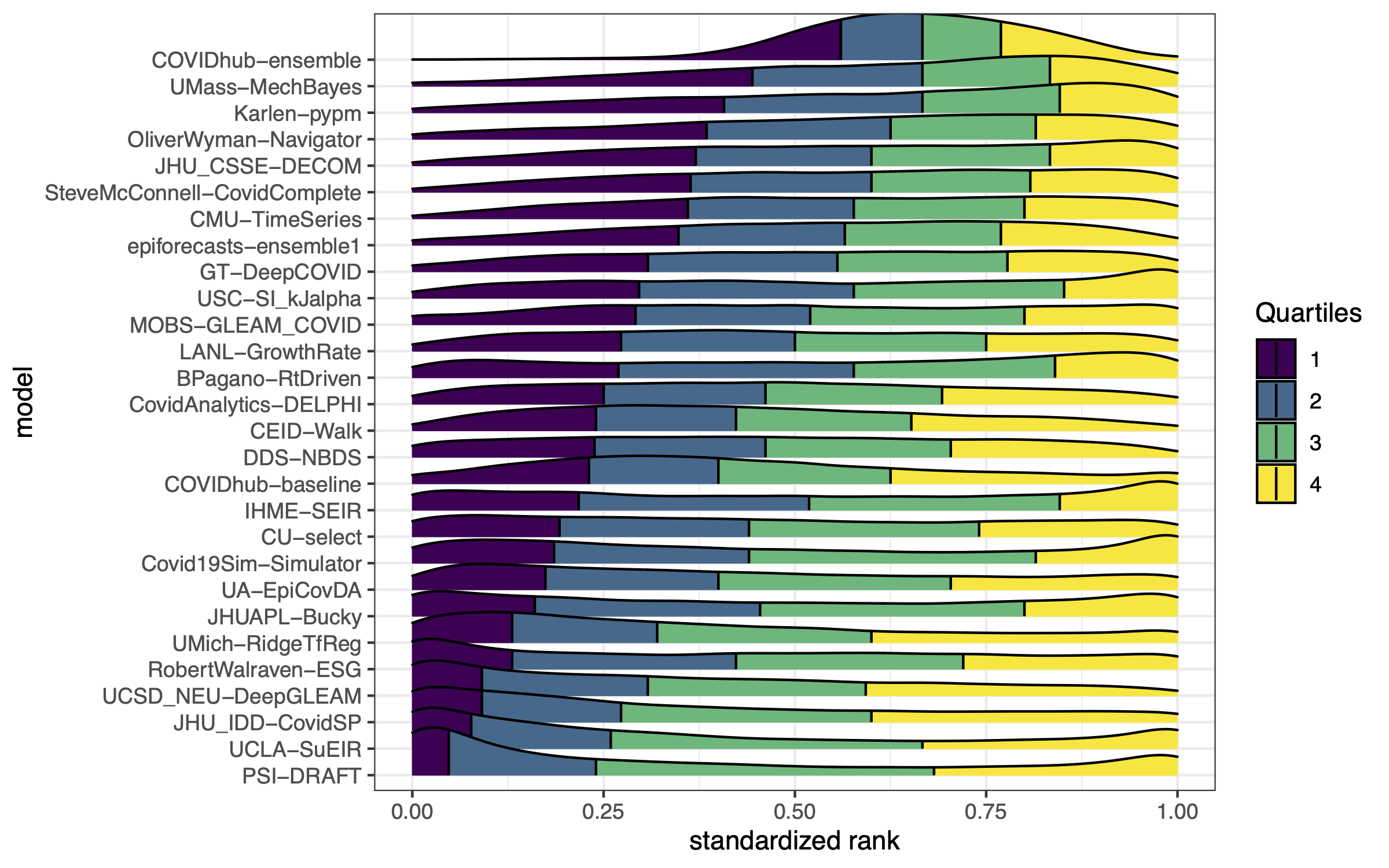
Two key goals of ensembling

1 Compete-with-best: ensemble should have accuracy competitive with best individual constituent model

  1. Robustness-over-all: ensemble should have greater robustness than any individual constituent model

Typically these are hard to accomplish simultaneously, and untrained methods excel at point 2, whereas trained methods can achieve point 1

Linear stacking

One of the simplest trained ensemble methods is to directly fit a weighted combination of base forecasts to optimize accuracy (MSE, MAE, etc.), often called linear stacking: e.g., to form the forecast at time \(t\), we solve

\[\begin{alignat*}{2} &\min_{w \in \R^p} && \hspace{-6pt} \sum_{s=t_0+1}^t \bigg( y_s - \sum_{j=1}^p w_j \cdot \hat{y}^j_{s|s-h} \bigg)^2 \\ &\st \quad && \sum_{j=1}^p w_j = 1, \;\;\text{and} \;\; w_j \geq 0, \; j=1,\dots,p \end{alignat*}\]

then use

\[ \hat{y}^{\text{stack}}_{t+h|t} = \sum_{j=1}^p \hat{w}^t_j \cdot \hat{y}^j_{t+h|t} \]

Note that the stacking optimization problem uses forward-looking predictions (as in time series cross-validation)

Recalibration

  • We have seen that prediction intervals often have empirical coverage << nominal coverage, e.g., our 80% predictive intervals in practice cover \(\approx\) 60% of the time

  • Recalibration methods aim at adjusting the intervals so that nominal coverage \(\approx\) empirical coverage

Quantile tracking

Quantile tracking is a method for producing calibrated prediction intervals from base forecasts and scores. In the simplest case, we can take the score to be absolute error of point forecasts:

\[e_t = |y_t - \hat y_{t|t-1}|\]

  • Let \(\hat q_{t}^{1-\alpha}\) be a predicted level \(1-\alpha\) quantile of the distribution of \(e_t\)

  • Define \(I_{t|t-1}^{1-\alpha} = [\hat{y}_{t|t-1} - \hat{q}_t^{1-\alpha}, \; \hat{y}_{t|t-1} + \hat{q}_t^{1-\alpha}]\). Note that

    \[ e_t \leq \hat{q}_t^{1-\alpha} \iff y_t \in I_{t|t-1}^{1-\alpha} \]

  • Therefore we the reduced the problem of producing prediction intervals \(I_{t|t-1}^{1-\alpha}\) to one of tracking a quantile of \(e_t\)

Quantile updates

We begin with some estimate \(\hat{q}_{t_0+1}^{1-\alpha}\) based on a burn-in set. Then repeat the following updates as \(t\) increases, for a step size \(\eta > 0\):

\[\hat q_{t+1}^{1-\alpha} = \begin{cases} \hat q_{t}^{1-\alpha} + \eta(1-\alpha) \quad \text{if } y_t\notin I_{t|t-1}^{1-\alpha} \\ \hat q_{t}^{1-\alpha} - \eta\alpha \quad \quad \quad \,\,\, \text{if } y_t\in I_{t|t-1}^{1-\alpha} \end{cases}\]

In words:

  • if the latest interval does not cover, then we increase the quantile (make the next interval wider),
  • otherwise we decrease the quantile by (make the next interval narrower).

This method has the following guarantee:

\[ \Bigg| \frac{1}{T} \sum_{t=t_0+1}^{t_0+T} 1 \big\{ y_t \in I_{t|t-1}^{1-\alpha} \big\} - (1-\alpha) \Bigg| \leq \frac{b/\eta + 1}{T} \]

where \(b\) is a bound on the errors (largest error possible/observable).

Multi-horizon smoothing