Using epipredict on non-epidemic panel data • epipredict

library(dplyr)
library(tidyr)
library(parsnip)
library(recipes)
library(epiprocess)
library(epipredict)
library(epidatasets)
library(ggplot2)
theme_set(theme_bw())

Panel data, or longitudinal data, contain cross-sectional measurements of subjects over time. The epipredict package is most suitable for running forecasters on epidemiological panel data. An example of this is the covid_case_death_rates dataset, which contains daily state-wise measures of case_rate and death_rate for COVID-19 in 2021:

head(covid_case_death_rates, 3)
#> An `epi_df` object, 3 x 4 with metadata:
#> * geo_type  = state
#> * time_type = day
#> * as_of     = 2022-05-31
#> 
#> # A tibble: 3 × 4
#>   geo_value time_value case_rate death_rate
#> * <chr>     <date>         <dbl>      <dbl>
#> 1 ak        2020-12-31      35.9      0.158
#> 2 al        2020-12-31      65.1      0.438
#> 3 ar        2020-12-31      66.0      1.27

epipredict functions work with data in epi_df format. Despite the stated goal and name of the package, other panel datasets are also valid candidates for epipredict functionality, as long as they are in epi_df format.

Example panel data overview

In this vignette, we will demonstrate using epipredict with employment panel data from Statistics Canada. We will be using Table 37-10-0115-01: Characteristics and median employment income of longitudinal cohorts of postsecondary graduates two and five years after graduation, by educational qualification and field of study (primary groupings).

The full dataset contains yearly median employment income two and five years after graduation, and number of graduates. The data is stratified by variables such as geographic region (Canadian province), education, and age group. The year range of the dataset is 2010 to 2017, inclusive. The full dataset also contains metadata that describes the quality of data collected. For demonstration purposes, we make the following modifications to get a subset of the full dataset:

Only keep provincial-level geographic region (the full data also has “Canada” as a region)
Only keep “good” or better quality data rows, as indicated by the STATUS column
Choose a subset of covariates and aggregate across the remaining ones. The chosen covariates are age group, and educational qualification.

To use this data with epipredict, we need to convert it into epi_df format using epiprocess::as_epi_df() with additional keys. In our case, the additional keys are age_group, and edu_qual. Note that in the above modifications, we encoded time_value as type integer. This lets us set time_type = "year", and ensures that lag and ahead modifications later on are using the correct time units. See the epiprocess::epi_df for a list of all the time_types available.

Now, we are ready to use grad_employ_subset with epipredict. Our epi_df contains 1,445 rows and 7 columns. Here is a quick summary of the columns in our epi_df:

time_value (time value): year in date format
geo_value (geo value): province in Canada
num_graduates (raw, time series value): number of graduates
med_income_2y (raw, time series value): median employment income 2 years after graduation
med_income_5y (raw, time series value): median employment income 5 years after graduation
age_group (key): one of two age groups, either 15 to 34 years, or 35 to 64 years
edu_qual (key): one of 32 unique educational qualifications, e.g., “Master’s diploma”

# Rename for simplicity
employ <- grad_employ_subset
sample_n(employ, 6)
#> An `epi_df` object, 6 x 7 with metadata:
#> * geo_type  = custom
#> * time_type = integer
#> * other_keys = age_group, edu_qual
#> * as_of     = 2024-09-18
#> 
#> # A tibble: 6 × 7
#>   geo_value        age_group      edu_qual           time_value num_graduates
#> * <chr>            <fct>          <fct>                   <int>         <dbl>
#> 1 Saskatchewan     35 to 64 years Undergraduate cer…       2016           120
#> 2 British Columbia 35 to 64 years Post-baccalaureat…       2017           240
#> 3 Saskatchewan     35 to 64 years Post-baccalaureat…       2012            10
#> 4 Quebec           15 to 34 years Master's certific…       2010            80
#> 5 British Columbia 35 to 64 years Career, technical…       2012          3060
#> 6 New Brunswick    35 to 64 years Career, technical…       2013           230
#> # ℹ 2 more variables: med_income_2y <dbl>, med_income_5y <dbl>

In the following sections, we will go over pre-processing the data in the epi_recipe framework, and fitting a model and making predictions within the epipredict framework and using the package’s canned forecasters.

Autoregressive (AR) model to predict number of graduates in a year

Pre-processing

As a simple example, let’s work with the num_graduates column for now. We will first pre-process by standardizing each numeric column by the total within each group of keys. We do this since those raw numeric values will vary greatly from province to province since there are large differences in population.

employ_small <- employ %>%
  group_by(geo_value, age_group, edu_qual) %>%
  # Select groups where there are complete time series values
  filter(n() >= 6) %>%
  mutate(
    num_graduates_prop = num_graduates / sum(num_graduates),
    med_income_2y_prop = med_income_2y / sum(med_income_2y),
    med_income_5y_prop = med_income_5y / sum(med_income_5y)
  ) %>%
  ungroup()
head(employ_small)
#> An `epi_df` object, 6 x 10 with metadata:
#> * geo_type  = custom
#> * time_type = integer
#> * other_keys = age_group, edu_qual
#> * as_of     = 2024-09-18
#> 
#> # A tibble: 6 × 10
#>   geo_value           age_group      edu_qual        time_value num_graduates
#> * <chr>               <fct>          <fct>                <int>         <dbl>
#> 1 Newfoundland and L… 15 to 34 years Career, techni…       2010           430
#> 2 Newfoundland and L… 35 to 64 years Career, techni…       2010           140
#> 3 Newfoundland and L… 15 to 34 years Career, techni…       2010           630
#> 4 Newfoundland and L… 35 to 64 years Career, techni…       2010           140
#> 5 Newfoundland and L… 15 to 34 years Undergraduate …       2010          1050
#> 6 Newfoundland and L… 35 to 64 years Undergraduate …       2010           130
#> # ℹ 5 more variables: med_income_2y <dbl>, med_income_5y <dbl>,
#> #   num_graduates_prop <dbl>, med_income_2y_prop <dbl>, …

Below is a visualization for a sample of the small data for British Columbia and Ontario. Note that some groups do not have any time series information since we filtered out all time series with incomplete dates.

employ_small %>%
  filter(geo_value %in% c("British Columbia", "Ontario")) %>%
  filter(grepl("degree", edu_qual, fixed = T)) %>%
  group_by(geo_value, time_value, edu_qual, age_group) %>%
  summarise(num_graduates_prop = sum(num_graduates_prop), .groups = "drop") %>%
  ggplot(aes(x = time_value, y = num_graduates_prop, color = geo_value)) +
  geom_line() +
  scale_colour_manual(values = c("Cornflowerblue", "Orange"), name = "") +
  facet_grid(rows = vars(edu_qual), cols = vars(age_group)) +
  xlab("Year") +
  ylab("Percentage of gratuates") +
  theme(legend.position = "bottom")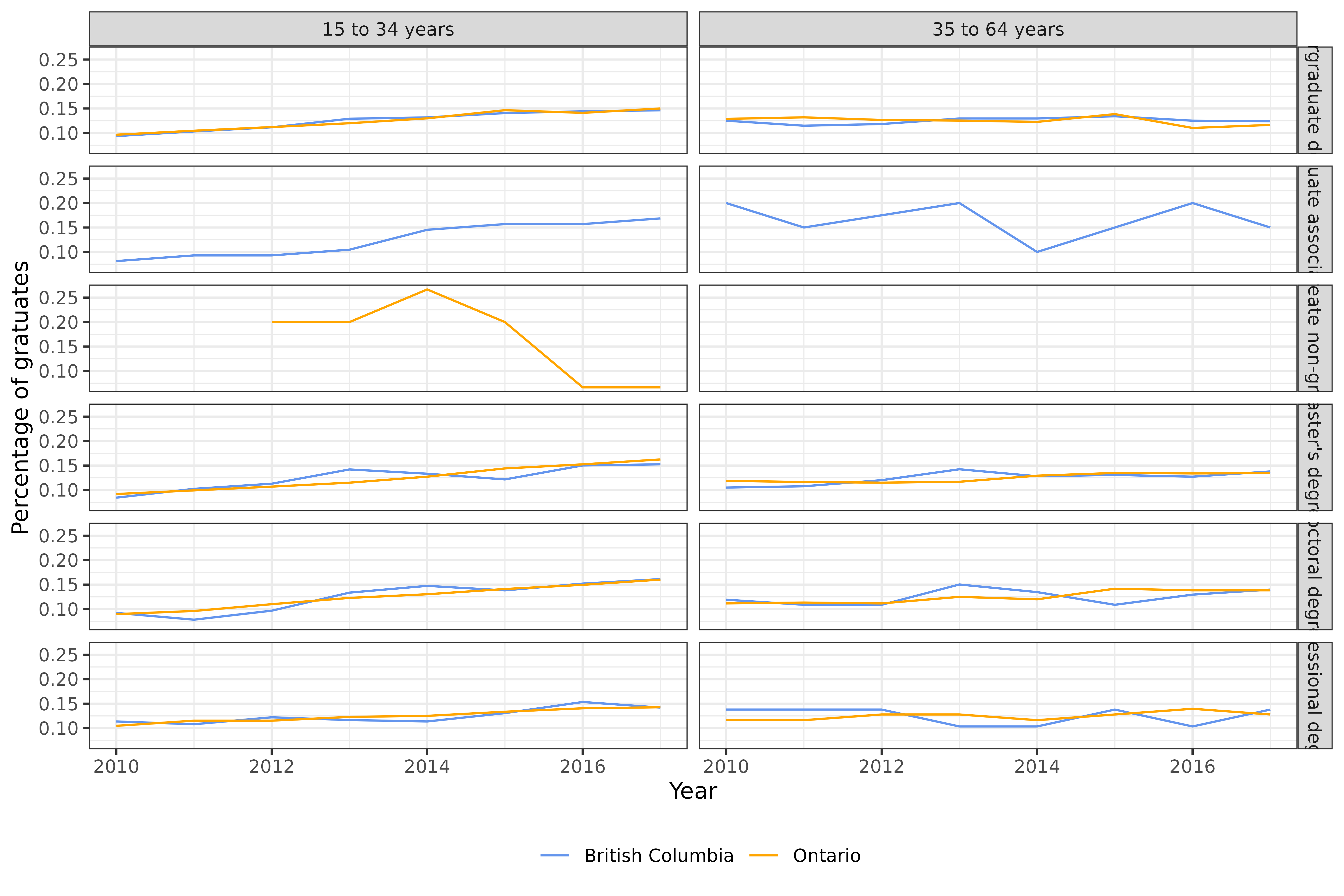

We will predict the standardized number of graduates (a proportion) in the next year (time $t+1$ ) using an autoregressive model with three lags (i.e., an AR(3) model). Such a model is represented algebraically like this:

$y_{t+1,ijk} = \alpha_0 + \alpha_1 y_{tijk} + \alpha_2 y_{t-1,ijk} + \alpha_3 y_{t-2,ijk} + \epsilon_{tijk}$

where $y_{tij}$ is the proportion of graduates at time $t$ in location $i$ and age group $j$ with education quality $k$ .

In the pre-processing step, we need to create additional columns in employ for each of $y_{t+1,ijk}$ , $y_{tijk}$ , $y_{t-1,ijk}$ , and $y_{t-2,ijk}$ . We do this via an epi_recipe. Note that creating an epi_recipe alone doesn’t add these outcome and predictor columns; the recipe just stores the instructions for adding them.

Our epi_recipe should add one ahead column representing $y_{t+1,ijk}$ and 3 lag columns representing $y_{tijk}$ , $y_{t-1,ijk}$ , and $y_{t-2,ijk}$ (it’s more accurate to think of the 0th “lag” as the “current” value with 2 lags, but that’s not quite how the processing works). Also note that since we specified our time_type to be year, our lag and lead values are both in years.

r <- epi_recipe(employ_small) %>%
  step_epi_ahead(num_graduates_prop, ahead = 1) %>%
  step_epi_lag(num_graduates_prop, lag = 0:2) %>%
  step_epi_naomit()
r
#> 
#> ── Epi Recipe ───────────────────────────────────────────────────────────────
#> 
#> ── Inputs
#> Number of variables by role
#> raw:        6
#> key:        2
#> geo_value:  1
#> time_value: 1
#> 
#> ── Operations
#> 1. Leading: num_graduates_prop by 1
#> 2. Lagging: num_graduates_prop by 0, 1, 2
#> 3. • Removing rows with NA values in: all_predictors()
#> 4. • Removing rows with NA values in: all_outcomes()

Let’s apply this recipe using prep and bake to generate and view the lag and ahead columns.

# Display a sample of the pre-processed data
bake_and_show_sample <- function(recipe, data, n = 5) {
  recipe %>%
    prep(data) %>%
    bake(new_data = data) %>%
    sample_n(n)
}

r %>% bake_and_show_sample(employ_small)
#> An `epi_df` object, 5 x 14 with metadata:
#> * geo_type  = custom
#> * time_type = integer
#> * other_keys = age_group, edu_qual
#> * as_of     = 2024-09-18
#> 
#> # A tibble: 5 × 14
#>   geo_value        age_group      edu_qual           time_value num_graduates
#> * <chr>            <fct>          <fct>                   <dbl>         <dbl>
#> 1 Ontario          35 to 64 years Master's diploma         2012            40
#> 2 British Columbia 15 to 34 years Undergraduate deg…       2014         11520
#> 3 Alberta          35 to 64 years Career, technical…       2013          1270
#> 4 Alberta          35 to 64 years Undergraduate deg…       2016          1050
#> 5 Quebec           15 to 34 years Career, technical…       2016          3920
#> # ℹ 9 more variables: med_income_2y <dbl>, med_income_5y <dbl>,
#> #   num_graduates_prop <dbl>, med_income_2y_prop <dbl>, …

We can see that the prep and bake steps created new columns according to our epi_recipe:

ahead_1_num_graduates_prop corresponds to $y_{t+1,ijk}$
lag_0_num_graduates_prop, lag_1_num_graduates_prop, and lag_2_num_graduates_prop correspond to $y_{tijk}$ , $y_{t-1,ijk}$ , and $y_{t-2,ijk}$ respectively.

Model fitting and prediction

Since our goal for now is to fit a simple autoregressive model, we can use parsnip::linear_reg() with the default engine lm, which fits a linear regression using ordinary least squares.

We will use epi_workflow with the epi_recipe we defined in the pre-processing section along with the parsnip::linear_reg() model. Note that epi_workflow is a container and doesn’t actually do the fitting. We have to pass the workflow into fit() to get our estimated model coefficients $\widehat{\alpha}_i,\ i=0,...,3$ .

wf_linreg <- epi_workflow(r, linear_reg()) %>%
  fit(employ_small)
summary(extract_fit_engine(wf_linreg))
#> 
#> Call:
#> stats::lm(formula = ..y ~ ., data = data)
#> 
#> Residuals:
#>       Min        1Q    Median        3Q       Max 
#> -0.104501 -0.013043 -0.002708  0.009289  0.210582 
#> 
#> Coefficients:
#>                           Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)               0.108532   0.006695  16.211  < 2e-16 ***
#> lag_0_num_graduates_prop  0.324251   0.037163   8.725  < 2e-16 ***
#> lag_1_num_graduates_prop  0.014190   0.038543   0.368 0.712848    
#> lag_2_num_graduates_prop -0.137378   0.036337  -3.781 0.000168 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.02993 on 777 degrees of freedom
#> Multiple R-squared:  0.1084, Adjusted R-squared:  0.1049 
#> F-statistic: 31.47 on 3 and 777 DF,  p-value: < 2.2e-16

This output tells us the coefficients of the fitted model; for instance, the estimated intercept is $\widehat{\alpha}_0 =$ 0.109 and the coefficient for $y_{tijk}$ is $\widehat\alpha_1 =$ 0.324. The summary also tells us that all estimated coefficients are significantly different from zero. Extracting the 95% confidence intervals for the coefficients also leads us to the same conclusion: all the coefficient estimates are significantly different from 0.

confint(extract_fit_engine(wf_linreg))
#>                                2.5 %      97.5 %
#> (Intercept)               0.09538942  0.12167466
#> lag_0_num_graduates_prop  0.25130008  0.39720211
#> lag_1_num_graduates_prop -0.06147071  0.08985152
#> lag_2_num_graduates_prop -0.20870743 -0.06604791

Now that we have our workflow, we can generate predictions from a subset of our data. For this demo, we will predict the number of graduates using the last 2 years of our dataset.

latest <- get_test_data(recipe = r, x = employ_small)
preds <- stats::predict(wf_linreg, latest) %>% filter(!is.na(.pred))
# Display a sample of the prediction values, excluding NAs
preds %>% sample_n(5)
#> An `epi_df` object, 5 x 5 with metadata:
#> * geo_type  = custom
#> * time_type = integer
#> * other_keys = geo_value, age_group, edu_qual, time_value
#> * as_of     = 2024-09-18
#> 
#> # A tibble: 5 × 5
#>   geo_value                 age_group      edu_qual          time_value .pred
#> * <chr>                     <fct>          <fct>                  <dbl> <dbl>
#> 1 New Brunswick             15 to 34 years Professional deg…       2017 0.141
#> 2 British Columbia          15 to 34 years Career, technica…       2017 0.134
#> 3 Nova Scotia               15 to 34 years Master's degree         2017 0.133
#> 4 Ontario                   15 to 34 years Undergraduate ce…       2017 0.161
#> 5 Newfoundland and Labrador 15 to 34 years Master's degree         2017 0.139

We can do this using the augment function too. Note that predict and augment both still return an epiprocess::epi_df with all of the keys that were present in the original dataset.

augment(wf_linreg, latest) %>% sample_n(5)
#> An `epi_df` object, 5 x 11 with metadata:
#> * geo_type  = custom
#> * time_type = integer
#> * other_keys = geo_value, age_group, edu_qual, time_value
#> * as_of     = 2024-09-18
#> 
#> # A tibble: 5 × 11
#>   geo_value        age_group      edu_qual                  time_value  .pred
#> * <chr>            <fct>          <fct>                          <dbl>  <dbl>
#> 1 British Columbia 35 to 64 years Post-baccalaureate non-g…       2017  0.143
#> 2 Saskatchewan     15 to 34 years Career, technical or pro…       2015 NA    
#> 3 Manitoba         15 to 34 years Career, technical or pro…       2016 NA    
#> 4 Saskatchewan     35 to 64 years Doctoral degree                 2017  0.135
#> 5 Manitoba         35 to 64 years Other career, technical …       2016 NA    
#> # ℹ 6 more variables: num_graduates <dbl>, med_income_2y <dbl>,
#> #   med_income_5y <dbl>, num_graduates_prop <dbl>, …

Model diagnostics

First, we’ll plot the residuals (that is, $y_{tijk} - \widehat{y}_{tijk}$ ) against the fitted values ( $\widehat{y}_{tijk}$ ).

par(mfrow = c(2, 2), mar = c(5, 3, 1.2, 0))
plot(extract_fit_engine(wf_linreg))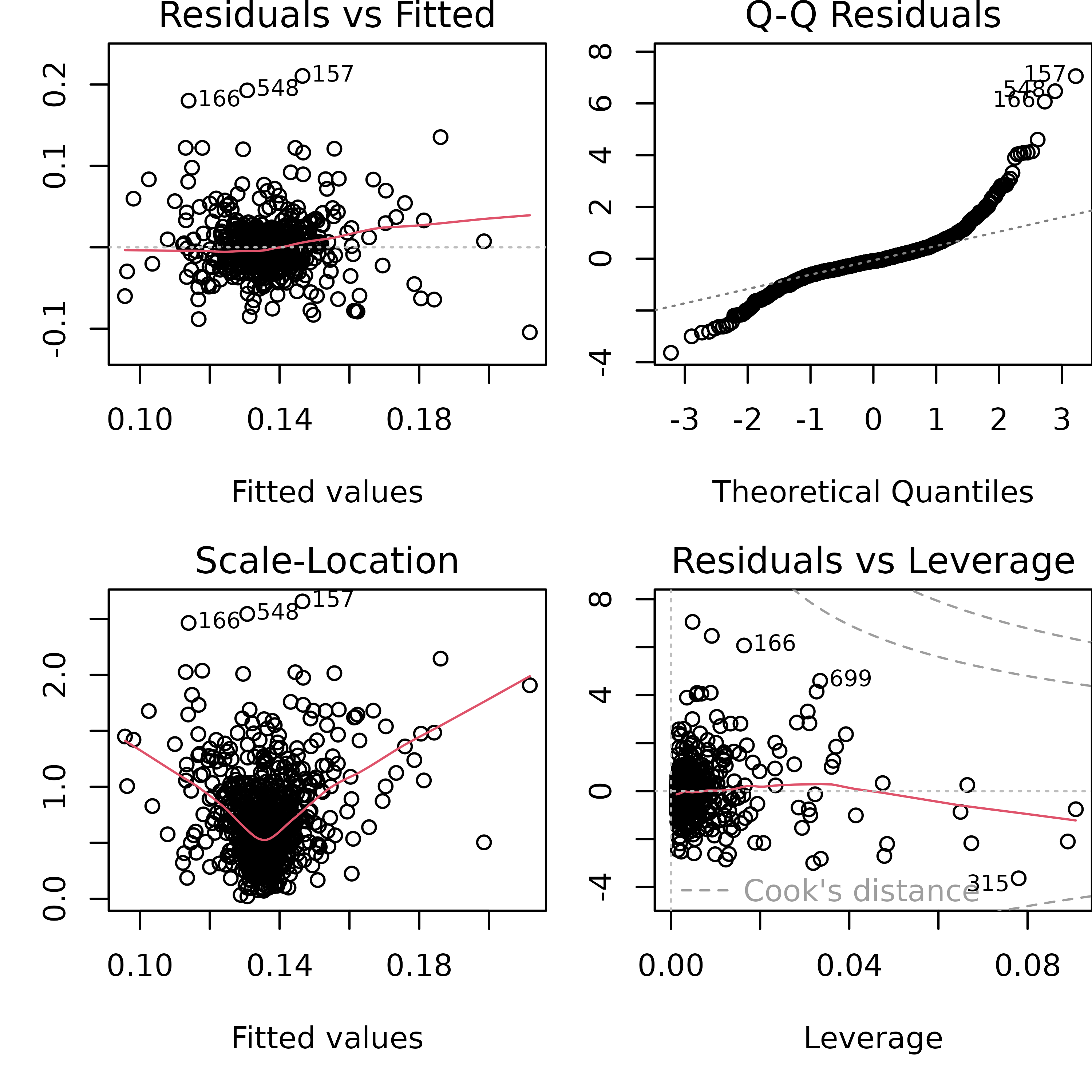

The fitted values vs. residuals plot shows us that the residuals are mostly clustered around zero, but do not form an even band around the zero line, indicating that the variance of the residuals is not constant. Additionally, the fitted values vs. square root of standardized residuals makes this more obvious - the spread of the square root of standardized residuals varies with the fitted values.

The Q-Q plot shows us that the residuals have heavier tails than a Normal distribution. So the normality of residuals assumption doesn’t hold either.

Finally, the residuals vs. leverage plot shows us that we have a few influential points based on the Cook’s distance (those outside the red dotted line).

Since we appear to be violating the linear model assumptions, we might consider transforming our data differently, or considering a non-linear model, or something else.

AR model with exogenous inputs

Now suppose we want to model the 1-step-ahead 5-year employment income using current and two previous values, while also incorporating information from the other two time-series in our dataset: the 2-year employment income and the number of graduates in the previous 2 years. We would do this using an autoregressive model with exogenous inputs, defined as follows:

$\begin{aligned} y_{t+1,ijk} &= \alpha_0 + \alpha_1 y_{tijk} + \alpha_2 y_{t-1,ijk} + \alpha_3 y_{t-2,ijk}\\ &\quad + \beta_1 x_{tijk} + \beta_2 x_{t-1,ijk}\\ &\quad + \gamma_2 z_{tijk} + \gamma_2 z_{t-1,ijk} + \epsilon_{tijk} \end{aligned}$

where $y_{tijk}$ is the 5-year median income (proportion) at time $t$ (in location $i$ , age group $j$ with education quality $k$ ), $x_{tijk}$ is the 2-year median income (proportion) at time $t$ , and $z_{tijk}$ is the number of graduates (proportion) at time $t$ .

Pre-processing

Again, we construct an epi_recipe detailing the pre-processing steps.

rx <- epi_recipe(employ_small) %>%
  step_epi_ahead(med_income_5y_prop, ahead = 1) %>%
  # 5-year median income has current, and two lags c(0, 1, 2)
  step_epi_lag(med_income_5y_prop, lag = 0:2) %>%
  # But the two exogenous variables have current values, and 1 lag c(0, 1)
  step_epi_lag(med_income_2y_prop, lag = c(0, 1)) %>%
  step_epi_lag(num_graduates_prop, lag = c(0, 1)) %>%
  step_epi_naomit()

bake_and_show_sample(rx, employ_small)
#> An `epi_df` object, 5 x 18 with metadata:
#> * geo_type  = custom
#> * time_type = integer
#> * other_keys = age_group, edu_qual
#> * as_of     = 2024-09-18
#> 
#> # A tibble: 5 × 18
#>   geo_value           age_group      edu_qual        time_value num_graduates
#> * <chr>               <fct>          <fct>                <dbl>         <dbl>
#> 1 Prince Edward Isla… 35 to 64 years Undergraduate …       2017            10
#> 2 British Columbia    35 to 64 years Post-baccalaur…       2014           180
#> 3 Alberta             35 to 64 years Career, techni…       2016          1250
#> 4 Saskatchewan        15 to 34 years Undergraduate …       2015          2600
#> 5 Saskatchewan        15 to 34 years Doctoral degree       2016            70
#> # ℹ 13 more variables: med_income_2y <dbl>, med_income_5y <dbl>,
#> #   num_graduates_prop <dbl>, med_income_2y_prop <dbl>, …

Model fitting & post-processing

Before fitting our model and making predictions, let’s add some post-processing steps using a few frosting layers to do a few things:

Threshold our predictions to 0. We are predicting proportions, which can’t be negative. And the transformed values back to dollars and people can’t be negative either.
Generate prediction intervals based on residual quantiles, allowing us to quantify the uncertainty associated with future predicted values.
Convert our predictions back to income values and number of graduates, rather than standardized proportions. We do this via the frosting layer layer_population_scaling().

# Create dataframe of the sums we used for standardizing
# Only have to include med_income_5y since that is our outcome
totals <- employ_small %>%
  group_by(geo_value, age_group, edu_qual) %>%
  summarise(med_income_5y_tot = sum(med_income_5y), .groups = "drop")

# Define post-processing steps
f <- frosting() %>%
  layer_predict() %>%
  layer_naomit(.pred) %>%
  layer_threshold(.pred, lower = 0) %>%
  # 90% prediction interval
  layer_residual_quantiles(
    quantile_levels = c(0.1, 0.9),
    symmetrize = FALSE
  ) %>%
  layer_population_scaling(
    .pred, .pred_distn,
    df = totals, df_pop_col = "med_income_5y_tot"
  )

wfx_linreg <- epi_workflow(rx, parsnip::linear_reg()) %>%
  fit(employ_small) %>%
  add_frosting(f)

summary(extract_fit_engine(wfx_linreg))
#> 
#> Call:
#> stats::lm(formula = ..y ~ ., data = data)
#> 
#> Residuals:
#>       Min        1Q    Median        3Q       Max 
#> -0.049668 -0.004509 -0.000516  0.004707  0.049882 
#> 
#> Coefficients:
#>                           Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)               0.041278   0.004975   8.298 4.72e-16 ***
#> lag_0_med_income_5y_prop  0.320780   0.049348   6.500 1.44e-10 ***
#> lag_1_med_income_5y_prop  0.079610   0.049116   1.621  0.10546    
#> lag_2_med_income_5y_prop  0.073048   0.033686   2.168  0.03043 *  
#> lag_0_med_income_2y_prop  0.118122   0.045579   2.592  0.00973 ** 
#> lag_1_med_income_2y_prop  0.034455   0.042749   0.806  0.42050    
#> lag_0_num_graduates_prop -0.025129   0.013603  -1.847  0.06509 .  
#> lag_1_num_graduates_prop  0.078268   0.013396   5.842 7.58e-09 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.01056 on 773 degrees of freedom
#> Multiple R-squared:  0.3224, Adjusted R-squared:  0.3163 
#> F-statistic: 52.54 on 7 and 773 DF,  p-value: < 2.2e-16

Based on the summary output for this model, we can examine confidence intervals and perform hypothesis tests as usual.

Let’s take a look at the predictions along with their 90% prediction intervals.

latest <- get_test_data(recipe = rx, x = employ_small)
predsx <- predict(wfx_linreg, latest)

# Display predictions along with prediction intervals
predsx %>%
  select(
    geo_value, time_value, edu_qual, age_group,
    .pred_scaled, .pred_distn_scaled
  ) %>%
  head() %>%
  pivot_quantiles_wider(.pred_distn_scaled)
#> # A tibble: 6 × 7
#>   geo_value            time_value edu_qual        age_group      .pred_scaled
#>   <chr>                     <dbl> <fct>           <fct>                 <dbl>
#> 1 Newfoundland and La…       2017 Career, techni… 15 to 34 years       45724.
#> 2 Newfoundland and La…       2017 Career, techni… 35 to 64 years       37614.
#> 3 Newfoundland and La…       2017 Career, techni… 15 to 34 years       56992.
#> 4 Newfoundland and La…       2017 Career, techni… 35 to 64 years       47802.
#> 5 Newfoundland and La…       2017 Post career, t… 15 to 34 years       61127.
#> 6 Newfoundland and La…       2017 Undergraduate … 15 to 34 years       72713.
#> # ℹ 2 more variables: `0.1` <dbl>, `0.9` <dbl>

Using canned forecasters

We’ve seen what we can do with non-epidemiological panel data using the recipes frame, with epi_recipe for pre-processing, epi_workflow for model fitting, and frosting for post-processing.

epipredict also comes with canned forecasters that do all of those steps behind the scenes for some simple models. Even though we aren’t working with epidemiological data, canned forecasters still work as expected, out of the box. We will demonstrate this with the simple flatline_forecaster and the direct autoregressive (AR) forecaster arx_forecaster.

For both illustrations, we will continue to use the employ_small dataset with the transformed numeric columns that are proportions within each group by the keys in our epi_df.

Flatline forecaster

In this first example, we’ll use flatline_forecaster to make a simple prediction of the 2-year median income for the next year, based on one previous time point. This model is representated algebraically as: $y_{t+1,ijk} = y_{tijk} + \epsilon_{tijk}$ where $y_{tijk}$ is the 2-year median income (proportion) at time $t$ .

out_fl <- flatline_forecaster(employ_small, "med_income_2y_prop",
  args_list = flatline_args_list(ahead = 1)
)

out_fl
#> ══ A basic forecaster of type flatline ══════════════════════════════════════
#> 
#> This forecaster was fit on 2024-11-12 19:18:06.
#> 
#> Training data was an <epi_df> with:
#> • Geography: custom,
#> • Other keys: age_group and edu_qual,
#> • Time type: integer,
#> • Using data up-to-date as of: 2024-09-18.
#> • With the last data available on 2017
#> 
#> ── Predictions ──────────────────────────────────────────────────────────────
#> 
#> A total of 167 predictions are available for
#> • 11 unique geographic regions,
#> • At forecast dates: 2017,
#> • For target dates: 2018,
#>

Autoregressive forecaster with exogenous inputs

In this second example, we’ll use arx_forecaster to make a prediction of the 5-year median income based using two lags, and using two lags on two exogenous variables: 2-year median income and number of graduates.

The canned forecaster gives us a simple way of making this forecast since it defines the recipe, workflow, and post-processing steps behind the scenes. This is very similar to the model we introduced in the “Autoregressive Linear Model with Exogenous Inputs” section of this article, but where all inputs have the same number of lags.

arx_args <- arx_args_list(lags = c(0L, 1L), ahead = 1L)

out_arx_lr <- arx_forecaster(employ_small, "med_income_5y_prop",
  c("med_income_5y_prop", "med_income_2y_prop", "num_graduates_prop"),
  args_list = arx_args
)

out_arx_lr
#> ══ A basic forecaster of type ARX Forecaster ════════════════════════════════
#> 
#> This forecaster was fit on 2024-11-12 19:18:07.
#> 
#> Training data was an <epi_df> with:
#> • Geography: custom,
#> • Other keys: age_group and edu_qual,
#> • Time type: integer,
#> • Using data up-to-date as of: 2024-09-18.
#> • With the last data available on 2017
#> 
#> ── Predictions ──────────────────────────────────────────────────────────────
#> 
#> A total of 166 predictions are available for
#> • 11 unique geographic regions,
#> • At forecast dates: 2017,
#> • For target dates: 2018,
#>

Other changes to the direct AR forecaster, like changing the engine, also work as expected. Below we use a boosted tree model instead of a linear regression.

out_arx_rf <- arx_forecaster(
  employ_small, "med_income_5y_prop",
  c("med_income_5y_prop", "med_income_2y_prop", "num_graduates_prop"),
  trainer = parsnip::boost_tree(mode = "regression", trees = 20),
  args_list = arx_args
)

out_arx_rf
#> ══ A basic forecaster of type ARX Forecaster ════════════════════════════════
#> 
#> This forecaster was fit on 2024-11-12 19:18:09.
#> 
#> Training data was an <epi_df> with:
#> • Geography: custom,
#> • Other keys: age_group and edu_qual,
#> • Time type: integer,
#> • Using data up-to-date as of: 2024-09-18.
#> • With the last data available on 2017
#> 
#> ── Predictions ──────────────────────────────────────────────────────────────
#> 
#> A total of 166 predictions are available for
#> • 11 unique geographic regions,
#> • At forecast dates: 2017,
#> • For target dates: 2018,
#>

Conclusion

While the purpose of epipredict is to allow tidymodels to operate on epidemiology data, it can be easily adapted (both the workflows and the canned forecasters) to work for generic panel data modelling.