Slide a computation over signal values

A central tool in the epiprocess package is epi_slide(), which is based on the powerful functionality provided in the slider package. In epiprocess, to “slide” means to apply a computation—represented as a function or formula—over a sliding/rolling data window. The function always applies the slide inside each group and the grouping is assumed to be across all group keys of the epi_df (this is the grouping used by default if you do not group the epi_df with a group_by()).

By default, the .window_size units depend on the time_type of the epi_df, which is determined from the types in the time_value column of the epi_df. See the “Details” in epi_slide() for more.

As in getting started guide, we’ll fetch daily reported COVID-19 cases from CA, FL, NY, and TX (note: here we’re using new, not cumulative cases) using the epidatr package, and then convert this to epi_df format.

library(epidatr)
library(epiprocess)
library(dplyr)

The data is fetched with the following query:

edf <- pub_covidcast(
  source = "jhu-csse",
  signals = "confirmed_incidence_num",
  geo_type = "state",
  time_type = "day",
  geo_values = "ca,fl,ny,tx,ga,pa",
  time_values = epirange(20200301, 20211231),
) %>%
  select(geo_value, time_value, cases = value) %>%
  arrange(geo_value, time_value) %>%
  as_epi_df()

The data has 2,684 rows and 3 columns.

Optimized rolling mean and sums

For the two most common sliding operations, we offer two optimized versions: epi_slide_mean() and epi_slide_sum(). This example gets the 7-day trailing average of the daily cases. Note that the name of the column(s) that we want to average is specified as the first argument of epi_slide_mean().

edf %>%
  group_by(geo_value) %>%
  epi_slide_mean("cases", .window_size = 7, na.rm = TRUE) %>%
  ungroup() %>%
  head(10)

## An `epi_df` object, 10 x 4 with metadata:
## * geo_type  = state
## * time_type = day
## * as_of     = 2024-08-23 02:40:48.296938
## 
## # A tibble: 10 × 4
##    geo_value time_value cases slide_value_cases
##  * <chr>     <date>     <dbl>             <dbl>
##  1 ca        2020-03-01     6              6   
##  2 ca        2020-03-02     4              5   
##  3 ca        2020-03-03     6              5.33
##  4 ca        2020-03-04    11              6.75
##  5 ca        2020-03-05    10              7.4 
##  6 ca        2020-03-06    18              9.17
##  7 ca        2020-03-07    26             11.6 
##  8 ca        2020-03-08    19             13.4 
##  9 ca        2020-03-09    23             16.1 
## 10 ca        2020-03-10    22             18.4

Note that we passed na.rm = TRUE to data.table::frollmean() via ... to epi_slide_mean.

The following computes the 7-day trailing sum of daily cases (and passed na.rm to data.table::frollsum() similarly):

edf %>%
  group_by(geo_value) %>%
  epi_slide_sum("cases", .window_size = 7, na.rm = TRUE) %>%
  ungroup() %>%
  head(10)

## An `epi_df` object, 10 x 4 with metadata:
## * geo_type  = state
## * time_type = day
## * as_of     = 2024-08-23 02:40:48.296938
## 
## # A tibble: 10 × 4
##    geo_value time_value cases slide_value_cases
##  * <chr>     <date>     <dbl>             <dbl>
##  1 ca        2020-03-01     6                 6
##  2 ca        2020-03-02     4                10
##  3 ca        2020-03-03     6                16
##  4 ca        2020-03-04    11                27
##  5 ca        2020-03-05    10                37
##  6 ca        2020-03-06    18                55
##  7 ca        2020-03-07    26                81
##  8 ca        2020-03-08    19                94
##  9 ca        2020-03-09    23               113
## 10 ca        2020-03-10    22               129

General sliding with a formula

The previous computations can also be performed using epi_slide(), which can be used for more general sliding computations (but is much slower for the specific cases of mean and sum).

The same 7-day trailing average of daily cases can be computed by passing in a formula for the first argument of epi_slide():

edf %>%
  group_by(geo_value) %>%
  epi_slide(~ mean(.x$cases, na.rm = TRUE), .window_size = 7) %>%
  ungroup() %>%
  head(10)

## An `epi_df` object, 10 x 4 with metadata:
## * geo_type  = state
## * time_type = day
## * as_of     = 2024-08-23 02:40:48.296938
## 
## # A tibble: 10 × 4
##    geo_value time_value cases slide_value
##  * <chr>     <date>     <dbl>       <dbl>
##  1 ca        2020-03-01     6        6   
##  2 ca        2020-03-02     4        5   
##  3 ca        2020-03-03     6        5.33
##  4 ca        2020-03-04    11        6.75
##  5 ca        2020-03-05    10        7.4 
##  6 ca        2020-03-06    18        9.17
##  7 ca        2020-03-07    26       11.6 
##  8 ca        2020-03-08    19       13.4 
##  9 ca        2020-03-09    23       16.1 
## 10 ca        2020-03-10    22       18.4

If your formula returns a data.frame, then the columns of the data.frame will be unpacked into the resulting epi_df. For example, the following computes the 7-day trailing average of daily cases and the 7-day trailing sum of daily cases:

edf %>%
  group_by(geo_value) %>%
  epi_slide(
    ~ data.frame(cases_mean = mean(.x$cases, na.rm = TRUE), cases_sum = sum(.x$cases, na.rm = TRUE)),
    .window_size = 7
  ) %>%
  ungroup() %>%
  head(10)

## An `epi_df` object, 10 x 5 with metadata:
## * geo_type  = state
## * time_type = day
## * as_of     = 2024-08-23 02:40:48.296938
## 
## # A tibble: 10 × 5
##    geo_value time_value cases cases_mean cases_sum
##  * <chr>     <date>     <dbl>      <dbl>     <dbl>
##  1 ca        2020-03-01     6       6            6
##  2 ca        2020-03-02     4       5           10
##  3 ca        2020-03-03     6       5.33        16
##  4 ca        2020-03-04    11       6.75        27
##  5 ca        2020-03-05    10       7.4         37
##  6 ca        2020-03-06    18       9.17        55
##  7 ca        2020-03-07    26      11.6         81
##  8 ca        2020-03-08    19      13.4         94
##  9 ca        2020-03-09    23      16.1        113
## 10 ca        2020-03-10    22      18.4        129

Note that this formula has access to all non-grouping columns present in the original epi_df object and must refer to them with the prefix .x$.... As we can see, the function epi_slide() returns an epi_df object with a new column appended that contains the results (from sliding), named slide_value as the default.

Some other information is available in additional variables:

• .group_key is a one-row tibble containing the values of the grouping variables for the associated group
• .ref_time_value is the reference time value the time window was based on

# Returning geo_value in the formula
edf %>%
  group_by(geo_value) %>%
  epi_slide(~ .x$geo_value[[1]], .window_size = 7) %>%
  ungroup() %>%
  head(10)

## An `epi_df` object, 10 x 4 with metadata:
## * geo_type  = state
## * time_type = day
## * as_of     = 2024-08-23 02:40:48.296938
## 
## # A tibble: 10 × 4
##    geo_value time_value cases slide_value
##  * <chr>     <date>     <dbl> <chr>      
##  1 ca        2020-03-01     6 ca         
##  2 ca        2020-03-02     4 ca         
##  3 ca        2020-03-03     6 ca         
##  4 ca        2020-03-04    11 ca         
##  5 ca        2020-03-05    10 ca         
##  6 ca        2020-03-06    18 ca         
##  7 ca        2020-03-07    26 ca         
##  8 ca        2020-03-08    19 ca         
##  9 ca        2020-03-09    23 ca         
## 10 ca        2020-03-10    22 ca

# Returning time_value in the formula
edf %>%
  group_by(geo_value) %>%
  epi_slide(~ .x$time_value[[1]], .window_size = 7) %>%
  ungroup() %>%
  head(10)

## An `epi_df` object, 10 x 4 with metadata:
## * geo_type  = state
## * time_type = day
## * as_of     = 2024-08-23 02:40:48.296938
## 
## # A tibble: 10 × 4
##    geo_value time_value cases slide_value
##  * <chr>     <date>     <dbl> <date>     
##  1 ca        2020-03-01     6 2020-02-24 
##  2 ca        2020-03-02     4 2020-02-25 
##  3 ca        2020-03-03     6 2020-02-26 
##  4 ca        2020-03-04    11 2020-02-27 
##  5 ca        2020-03-05    10 2020-02-28 
##  6 ca        2020-03-06    18 2020-02-29 
##  7 ca        2020-03-07    26 2020-03-01 
##  8 ca        2020-03-08    19 2020-03-02 
##  9 ca        2020-03-09    23 2020-03-03 
## 10 ca        2020-03-10    22 2020-03-04

While the computations above do not look very useful, these can be used as building blocks for computations that do something different depending on the geo_value or ref_time_value.

Slide the tidy way

Perhaps the most convenient way to setup a computation in epi_slide() is to pass in an expression for tidy evaluation. In this case, we can simply define the name of the new column directly as part of the expression, setting it equal to a computation in which we can access any columns of .x by name, just as we would in a call to dplyr::mutate(), or any of the dplyr verbs. For example:

slide_output <- edf %>%
  group_by(geo_value) %>%
  epi_slide(cases_7dav = mean(cases, na.rm = TRUE), .window_size = 7) %>%
  ungroup() %>%
  head(10)

In addition to referring to individual columns by name, you can refer to epi_df time window as .x (.group_key and .ref_time_value are still available). Also, the tidyverse “pronouns” .data and .env can also be used if you need distinguish between the data and environment.

As a simple sanity check, we visualize the 7-day trailing averages computed on top of the original counts:

library(ggplot2)
theme_set(theme_bw())

ggplot(slide_output, aes(x = time_value)) +
  geom_col(aes(y = cases, fill = geo_value), alpha = 0.5, show.legend = FALSE) +
  geom_line(aes(y = cases_7dav, col = geo_value), show.legend = FALSE) +
  facet_wrap(~geo_value, scales = "free_y") +
  scale_x_date(minor_breaks = "month", date_labels = "%b %y") +
  labs(x = "Date", y = "Reported COVID-19 cases")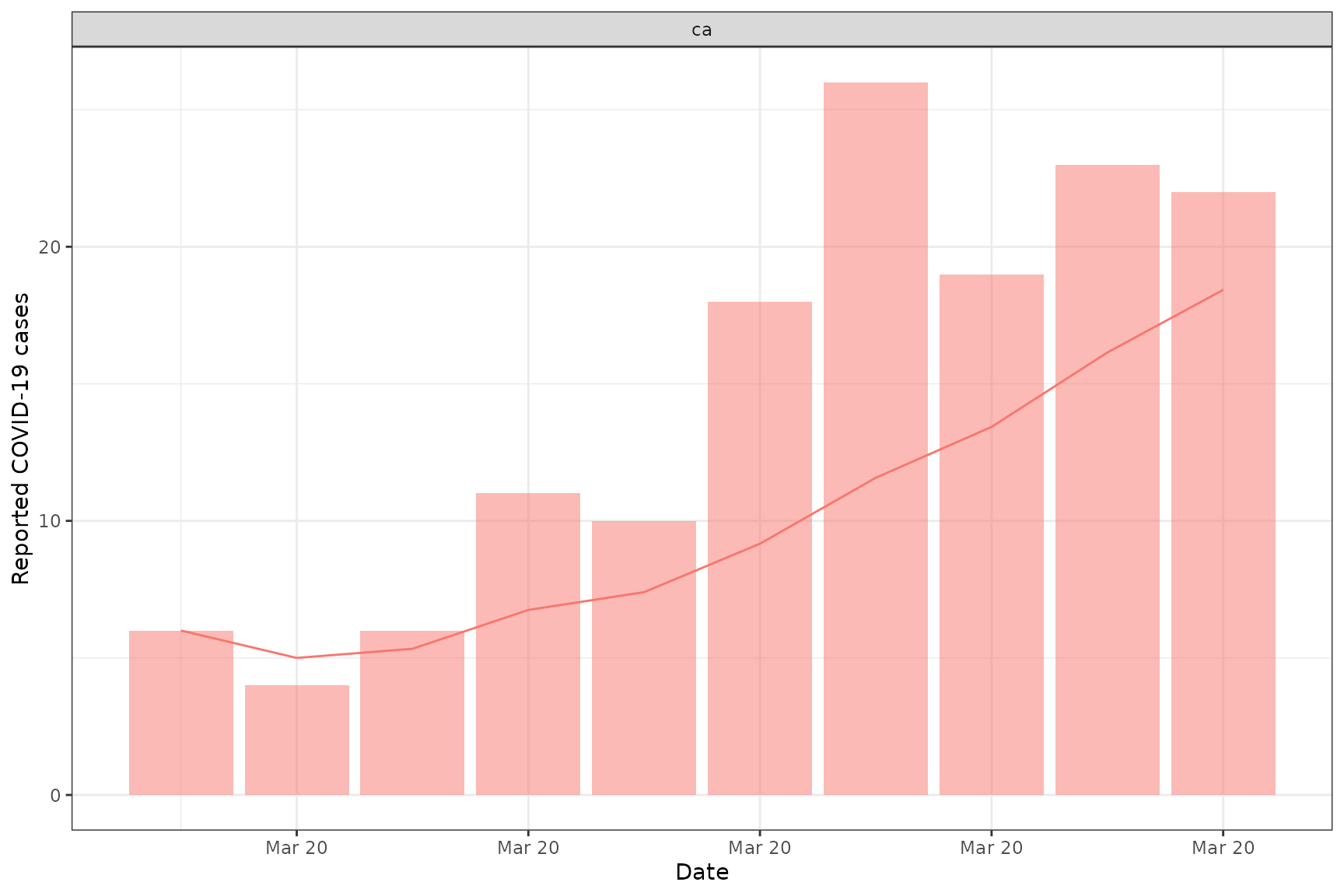

As we can see from the top right panel, it looks like Texas moved to weekly reporting of COVID-19 cases in summer of 2021.

Slide with a function

We can also pass a function to the second argument in epi_slide(). In this case, the passed function .f must have the form function(x, g, t, ...), where

• “x” is an epi_df with the same column names as the archive’s DT, minus the version column
• “g” is a one-row tibble containing the values of the grouping variables for the associated group
• “t” is the ref_time_value for the current window
• “…” are additional arguments

Recreating the last example of a 7-day trailing average:

edf %>%
  group_by(geo_value) %>%
  epi_slide(function(x, g, t) mean(x$cases, na.rm = TRUE), .window_size = 7) %>%
  ungroup() %>%
  head(10)

## An `epi_df` object, 10 x 4 with metadata:
## * geo_type  = state
## * time_type = day
## * as_of     = 2024-08-23 02:40:48.296938
## 
## # A tibble: 10 × 4
##    geo_value time_value cases slide_value
##  * <chr>     <date>     <dbl>       <dbl>
##  1 ca        2020-03-01     6        6   
##  2 ca        2020-03-02     4        5   
##  3 ca        2020-03-03     6        5.33
##  4 ca        2020-03-04    11        6.75
##  5 ca        2020-03-05    10        7.4 
##  6 ca        2020-03-06    18        9.17
##  7 ca        2020-03-07    26       11.6 
##  8 ca        2020-03-08    19       13.4 
##  9 ca        2020-03-09    23       16.1 
## 10 ca        2020-03-10    22       18.4

Running a simple autoregressive forecaster

As a more complex example, we create a forecaster based on an autoregression or AR model. AR models can be fit in numerous ways (using base R functions and various packages), but here we define it “by hand” both because it provides a more advanced example of sliding a function over an epi_df object, and because it allows us to be a bit more flexible in defining a probabilistic forecaster: one that outputs not just a point prediction, but a notion of uncertainty around this. In particular, our forecaster will output a point prediction along with an 90% uncertainty band, represented by a predictive quantiles at the 5% and 95% levels (lower and upper endpoints of the uncertainty band).

The function defined below, prob_ar(), is our probabilistic AR forecaster. The lagsargument indicates which lags to use in the model, and ahead indicates how far ahead in the future to make forecasts (both are encoded in terms of the units of the time_value column; so, days, in the working epi_df being considered in this vignette).

prob_ar <- function(y, lags = c(0, 7, 14), ahead = 6, min_train_window = 20,
                    lower_level = 0.05, upper_level = 0.95, symmetrize = TRUE,
                    intercept = FALSE, nonneg = TRUE) {
  # Return NA if insufficient training data
  if (length(y) < min_train_window + max(lags) + ahead) {
    return(data.frame(point = NA, lower = NA, upper = NA))
  }

  # Filter down the edge-NAs
  y <- y[!is.na(y)]

  # Build features and response for the AR model
  dat <- do.call(
    data.frame,
    purrr::map(lags, function(j) lag(y, n = j))
  )
  names(dat) <- paste0("x", seq_len(ncol(dat)))
  if (intercept) dat$x0 <- rep(1, nrow(dat))
  dat$y <- lead(y, n = ahead)

  # Now fit the AR model and make a prediction
  obj <- lm(y ~ . + 0, data = dat)
  point <- predict(obj, newdata = tail(dat, 1))

  # Compute a band
  r <- residuals(obj)
  s <- ifelse(symmetrize, -1, NA) # Should the residuals be symmetrized?
  q <- quantile(c(r, s * r), probs = c(lower_level, upper_level), na.rm = TRUE)
  lower <- point + q[1]
  upper <- point + q[2]

  # Clip at zero if we need to, then return
  if (nonneg) {
    point <- max(point, 0)
    lower <- max(lower, 0)
    upper <- max(upper, 0)
  }
  return(data.frame(point = point, lower = lower, upper = upper))
}

We go ahead and slide this AR forecaster over the working epi_df of COVID-19 cases. Note that we actually model the cases_7dav column, to operate on the scale of smoothed COVID-19 cases. This is clearly equivalent, up to a constant, to modeling weekly sums of COVID-19 cases.

fc_time_values <- seq(as.Date("2020-06-01"), as.Date("2021-12-01"), by = "1 months")
edf %>%
  group_by(geo_value) %>%
  epi_slide(cases_7dav = mean(.data$cases, na.rm = TRUE), .window_size = 7) %>%
  epi_slide(fc = prob_ar(.data$cases_7dav), .window_size = 120, .ref_time_values = fc_time_values) %>%
  ungroup() %>%
  head(10)

## An `epi_df` object, 10 x 5 with metadata:
## * geo_type  = state
## * time_type = day
## * as_of     = 2024-08-23 02:40:48.296938
## 
## # A tibble: 10 × 5
##    geo_value time_value cases cases_7dav fc$point $lower $upper
##  * <chr>     <date>     <dbl>      <dbl>    <dbl>  <dbl>  <dbl>
##  1 ca        2020-06-01  2437      2694     2973.  2566.  3380.
##  2 ca        2020-07-01  7346      6722     7892.  7321.  8462.
##  3 ca        2020-08-01  8616      8284.    7188.  6153.  8223.
##  4 ca        2020-09-01  4248      4707.    4133.  2329.  5937.
##  5 ca        2020-10-01  3504      3360.    3257.  1449.  5064.
##  6 ca        2020-11-01  4210      4441.    3840.  2258.  5422.
##  7 ca        2020-12-01 23626     15690    17699. 16082. 19316.
##  8 ca        2021-01-01 50251     41097.   45534. 38417. 52650.
##  9 ca        2021-02-01 13098     17952.   15266.  6725. 23808.
## 10 ca        2021-03-01  3031      5209     4482.     0  12982.

Note that here we have utilized an argument .ref_time_values to perform the sliding computation (here, compute a forecast) at a specific subset of reference time values (the start of every month from mid 2020 to the end of 2021). The resulting epi_df now contains three new columns: fc$point, fc$lower, and fc$upper corresponding to the point forecast, and the lower and upper endpoints of the 95% prediction band, respectively.

To finish off, we plot the forecasts at some times (spaced out by a few months) over the last year, at multiple horizons: 7, 14, 21, and 28 days ahead. To do so, we encapsulate the process of generating forecasts into a simple function, so that we can call it a few times.

# Note the use of .all_rows = TRUE (keeps all original rows in the output)
k_week_ahead <- function(x, ahead = 7) {
  x %>%
    group_by(geo_value) %>%
    epi_slide(cases_7dav = mean(.data$cases, na.rm = TRUE), .window_size = 7) %>%
    epi_slide(
      fc = prob_ar(.data$cases_7dav, ahead = ahead),
      .window_size = 120,
      .ref_time_values = fc_time_values,
      .all_rows = TRUE
    ) %>%
    ungroup() %>%
    mutate(target_date = .data$time_value + ahead)
}

# First generate the forecasts, and bind them together
z <- bind_rows(
  k_week_ahead(edf, ahead = 7),
  k_week_ahead(edf, ahead = 14),
  k_week_ahead(edf, ahead = 21),
  k_week_ahead(edf, ahead = 28)
)

# Now plot them, on top of actual COVID-19 case counts
ggplot(z) +
  geom_line(aes(x = time_value, y = cases_7dav), color = "gray50") +
  geom_ribbon(aes(
    x = target_date, ymin = fc$lower, ymax = fc$upper,
    group = time_value
  ), fill = 6, alpha = 0.4) +
  geom_line(aes(x = target_date, y = fc$point, group = time_value)) +
  geom_point(aes(x = target_date, y = fc$point, group = time_value),
    size = 0.5
  ) +
  geom_vline(
    data = tibble(x = fc_time_values), aes(xintercept = x),
    linetype = 2, alpha = 0.5
  ) +
  facet_wrap(vars(geo_value), scales = "free_y") +
  scale_x_date(minor_breaks = "month", date_labels = "%b %y") +
  labs(x = "Date", y = "Reported COVID-19 cases")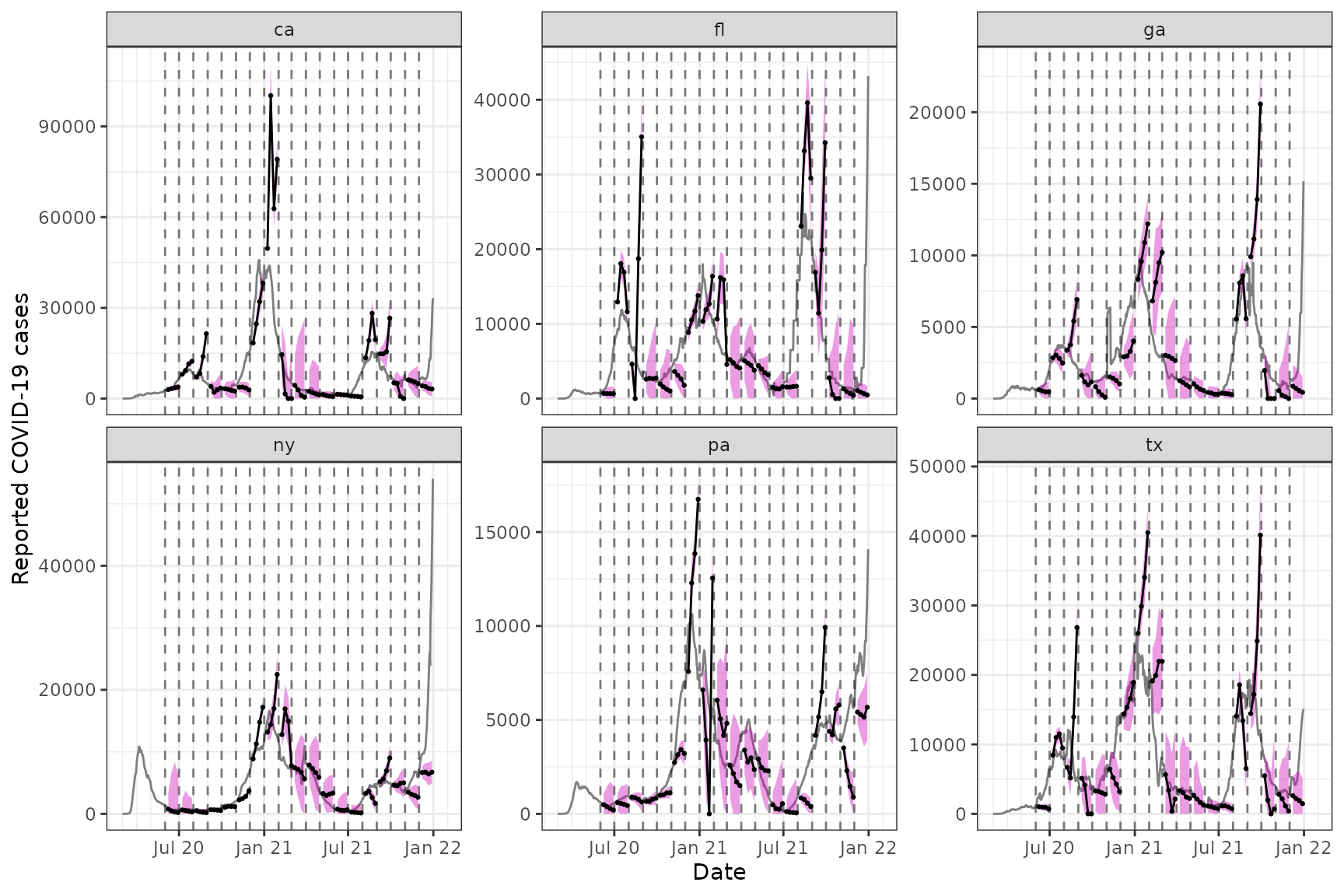

Two points are worth making. First, the AR model’s performance here is pretty spotty. At various points in time, we can see that its forecasts are volatile (its point predictions are all over the place), or overconfident (its bands are too narrow), or both at the same time. This is only meant as a simple demo and not entirely unexpected given the way the AR model is set up. The epipredict package, which is a companion package to epiprocess, offers a suite of predictive modeling tools that can improve on some of the shortcomings of the above simple AR model.

Second, the AR forecaster here is using finalized data, meaning, it uses the latest versions of signal values (reported COVID-19 cases) available, for both training models and making predictions historically. However, this is not reflective of the provisional nature of the data that it must cope with in a true forecast task. Training and making predictions on finalized data can lead to an overly optimistic sense of accuracy; see, for example, McDonald et al. (2021), and references therein. Fortunately, the epiprocess package provides a data structure called epi_archive that can be used to store all data revisions, and furthermore, an epi_archive object knows how to slide computations in the correct version-aware sense (for the computation at each reference time $t$, it uses only data that would have been available as of $t$). We will revisit this example in the archive vignette.

Attribution

The percent_cli data is a modified part of the COVIDcast Epidata API Doctor Visits data. This dataset is licensed under the terms of the Creative Commons Attribution 4.0 International license. Copyright Delphi Research Group at Carnegie Mellon University 2020.

This document contains a dataset that is a modified part of the COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University as republished in the COVIDcast Epidata API. This data set is licensed under the terms of the Creative Commons Attribution 4.0 International license by the Johns Hopkins University on behalf of its Center for Systems Science in Engineering. Copyright Johns Hopkins University 2020.

From the COVIDcast Epidata API: These signals are taken directly from the JHU CSSE COVID-19 GitHub repository without changes.